Some of the topics of my recent research

• Electron-positron cascades in pulsars

  I am studying electron-positron plasma generation in magnetospheres of pulsars starting from first principles using a hybrid Particle-In-Cell/Monte-Carlo numerical code.

• Force-free pulsar magnetosphere

  I developed what is up to now the most advanced model of the force-free magnetosphere of an aligned pulsar using a high-resolution multigrid numerical code specially developed for this task.

• Magnetar magnetosphere

  I and my collaborators developed an analytical model for the structure of the magnetosphere of an oscillating neutron star.

---

Electromagnetically driven electron-positron cascades

Electron-positron cascades play a central role in theory of radio pulsars — it is believed that radio pulsar "dies" when its rotation became so slow that cascades in the polar caps stop producing electron-positron plasma in the magnetosphere. Non-stationary regime of electromagnetically driven cascades has been poorly studied and all previous attempts to model time-dependent cascades relied on some simplifying assumptions. I decided to conduct a detailed study of dynamics of electron-positrons cascades starting from first principles and developed a numerical algorithm for self-consistent time-dependent kinetic simulation of electromagnetically driven electron-positron cascades — wherein particle acceleration, pair creation and screening of the electric field are calculated simultaneously — and wrote a hybrid Particle-In-Cell / Monte-Carlo code based on it.

I have already performed exhaustive self-consistent simulations of polar cap (PC) pair cascades in 1D. These simulations studied in detail both classes of pulsar PC cascade models: (i) those that do not allow charges to be extracted from the NS surface (Timokhin 2009, 2010), the model proposed by Ruderman & Sutherland (1975) and (ii) the more popular ones in which particles can freely leave the surface (Timokhin & Arons 2013), the Space Charge Limited Flow (SCLF) regime, first proposed by Arons & Scharlemann (1979).

Plasma flow with no particles extraction from the star

For the model when no particles can be extracted from the neutron star the cascade zone easily adjusts to the current density required by the magnetosphere and produces dense electron-positron plasma in accordance with qualitative expectations of the original model. But surprisingly, the pair formation turned out to be very regular, showing a limit cycle behavior with the electron-positron plasma having a thermalized low-energy component. Pair formation happens in bursts and each discharge also excites a coherent superluminal electrostatic plasma wave that might be important for the generation of pulsar radio emission. Formation of such wave is shown on the following video (full resolution video MP4, [6.7 MB]):

Video 1 Formation of a superluminal electrostatic wave. The top panel shows the phase portrait of the flow during active phase of pair formation - particle momenta normalized to $m_ec$ vs the distance from the NS. Electrons are shown as blue dots, positrons by red dots, and $\gamma$-rays by black dots; each dot is an individual numerical particle. The low panes shows the electric field in the domain. Vertical red lines are moving with the speed of light into the magnetosphere and are given for reference. Note that the phase velocity of electric field oscillations is larger than the speed of light.

Plasma flow with abundant particles supply from the star

In the case when particles can be freely extracted from the neutron star the cascade behavior turned out to be qualitatively different than expected in the being for a long time "standard" cascade models. The flow character depends on the ratio of the current density to the current density $J_{\rm{}GJ}\equiv\rho_{\rm{}GJ}c$, where $\rho_{\rm{}GJ}$ is the so-called Goldreich-Julian charge density - the characteristic charge density in the magnetosphere. For the field lines where the current density is smaller that the Goldreich-Julian current density $0< J/J_{\rm{}GJ}< 1$ no pair plasma is produced because the accelerating zone is very small due to an instability of the plasma flow. Plasma flow along these field lines can be described as a beam of mildly relativistic particles propagating through a cloud of trapped particles with near-thermal distribution, the plasma density is low and equal to the GJ charge density, $n=\rho_{\rm{}GJ}/e$. Formation of such low energetic flow is shown on the video below (full resolution video MP4, [8.2 MB]):

Video 2 Formation of a low energetic plasma flow, current density $J=J_{\rm{}GJ}/2$. Particles can bee freely extracted from the NS surface, simulation starts from vacuum configuration, there are no particles above the NS at first. The video shows phase portrait of the plasma: particle momenta $p_{-}$ normalized to $m_ec$ vs the distance from the NS. The distance from the NS (along the $x$-axis) is normalized to the Debye length of plasma with GJ charge density $\lambda_{\textrm{D}}\simeq2\,(B/10^{12})^{-1/2}P^{1/2}$ cm, ($B$ - pulsar magnetic field in G, $P$ - pulsar period in sec). Electrons are shown as blue dots, each dot is an individual numerical particle. Red dashed line is an analytical solution for plasma flow in one-fluid approximation.

Pair formation is possible only along field lines where the current density is either larger than the Goldreich-Julian current density (super-GJ flow, $J/J_{\rm{}GJ}> 1$) of has the opposite sign to it (anti-GJ flow, $J/J_{\rm{}GJ}< 0$). Pair creation is highly non-stationary, similar to discharges in the Ruderman-Sutherland model. The video below shows plasma flow for super-GJ current density (full resolution video MP4, [6.1 MB]):

Video 3 Phase portrait of super-GJ flow during active phase of pair formation - particle momenta normalized to $m_ec$ vs the distance from the NS. Electrons are shown as blue dots, positrons by red dots, $\gamma$-rays by black dots, and protons by magenta dots; each dot is an individual numerical particle. Gray regions on phase space plots show regions of the numerical domain where no pair creation is possible, they represent distant regions of the outer magnetosphere where cross-section of pair creation becomes negligible.

Overview of plasma flow regimes for SCLF

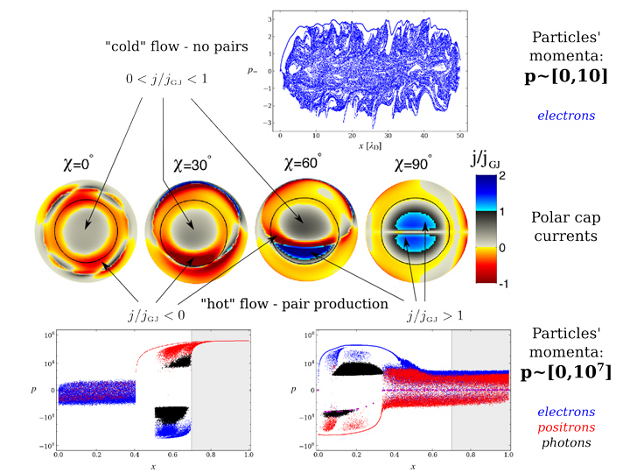
Figure 1 Current density distribution in the polar cap of pulsar for different pulsar inclination angles $a$ (central panel) and examples of particle distributions - phase portraits: the plot of particle momenta normalized to $m_ec$ vs the distance from the NS - for different cascade regimes in the space-charge limited flow model (top and bottom panels). Colors on the middle plot show the ratio of $J/J_{\rm{}GJ}$ and polar cap boundary is shown by a thin black circle on each subplot. In the phase portraits the distance from the NS (along the $x$-axis) is normalized to the width of the polar cap on the bottom plots, on the top plot the distance is normalized to the Debye length of plasma with GJ charge density $\lambda_{\textrm{D}}\simeq2\,(B/10^{12})^{-1/2}P^{1/2}$ cm, ($B$ - pulsar magnetic field in G, $P$ - pulsar period in sec). Electrons are shown as blue dots, positrons by red dots, and $\gamma$-rays by black dots. Gray regions on phase space plots show regions of the numerical domain where no pair creation is possible, they represent distant regions of the outer magnetosphere where cross-section of pair creation becomes negligible. Note that on the upper plot particles are only mildly relativistic and no pairs are produced (adapted from Timokhin & Arons 2013).

References

• Timokhin A. N. and Arons J., 2013, MNRAS, 429, 20 [ADS]
• Timokhin A. N., 2010, MNRAS, 408, 2092 [ADS]
• Timokhin A. N., 2009 Fermi Symposium eConf Proceedings C091122 (arXiv:0912.5475)

Force-free pulsar magnetosphere

Radio pulsars are highly magnetized rapidly rotating neutron stars. Most of pulsar emission is of non-thermal origin and is produced in the magnetosphere. Figuratively speaking, pulsars are shining electrical generators. Pulsar emission is beamed, and because of neutron star rotation the beam(s) crosses the line of sight at regular time intervals. The received radiation is in form of extremely regularly repeating pulses. The pulse peaks are narrow, what points to smallness of emitting regions, and, hence, to smallness of regions where particles are accelerated. The rest of the magnetosphere should be, therefore, "quiet", what together with other physical arguments makes a force-free magnetosphere model, introduced by Goldreich & Julian (1969), a natural "standard model" for pulsar magnetosphere.

I studied in detail properties of the force-free pulsar magnetosphere. I developed a high-resolution multigrid code for solution of the relativistic Grad-Shafranov equation describing force-free cylindrically-symmetric magnetic field of a rapidly rotating highly magnetized star (the so-called "pulsar equation"). I studied properties of differentially rotating pulsar magnetosphere using analytical models too. I found a set of solutions with different sizes of the closed magnetic field line zone. I have explicitly shown that the current density distribution in the force-free magnetosphere of an aligned pulsar in incompatible with the current theories of pair creation in the pulsar polar cap. I also found that the current sheet separating closed and open magnetic field lines has non-zero surface charge density.

On of the important results of these studies is that stationary unidirectional particle flow in the polar cap cascade zone cannot coexist with the the force-free pulsar magnetosphere, and, hence, models of electron-positron plasma generation in pulsar magnetospheres must be revised.

Figures below illustrate some of the obtained results

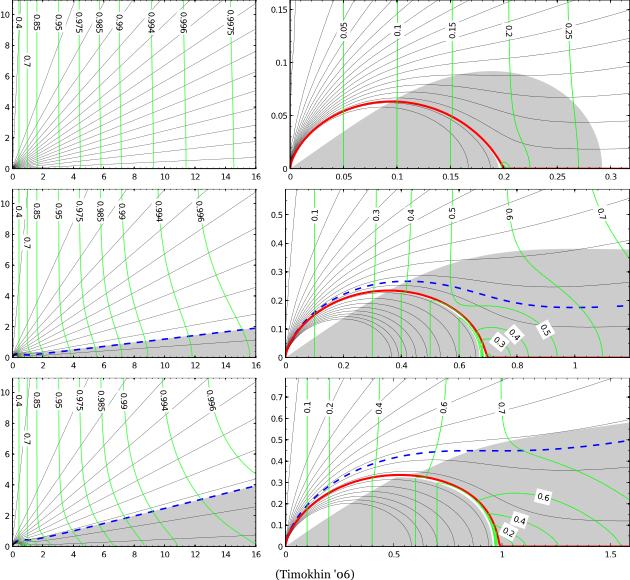
Figure 1 Global structure of the magnetosphere with different sizes of the corotating zone x₀=0.992 - top figures, x₀=0.7 - middle figures, x₀=0.2 - bottom figures. Magnetic field lines are shown by thin solid lines, the labeled green lines are contours of the plasma drift velocity (normalized to the speed of light), gray area is the domain where the Goldreich-Julian charge density is positive. Dashed line separates regions with direct (above the line) and return (below the line) volume currents. The boundary between open and closed magnetic field lines is shown by the thick solid line. On the left figures almost the whole calculation domain is shown, on the right figures - the central part of the calculation domain. Distances along x-axis (horizontal) and z-axis (vertical) are normalized to the radius of the light cylinder.

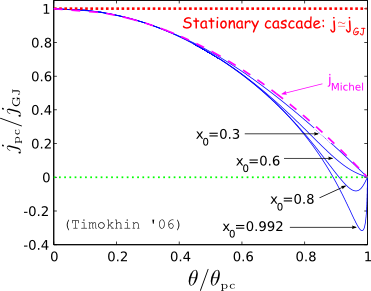
Figure 2 Current density distribution j_pc in the polar cap of pulsar as a function of the colatitude. j is normalized to the Goldreich-Julian current density j_GJ and the colatitude is measured in units of the colatitude of the polar cap boundary θ_pc. Different lines correspond to configurations with different sized of the closed field line zone x₀. The red dashed line indicates the current density distribution predicted by stationary theories of polar cap cascades. j_Michel is the current density in the split-monopole magnetosphere.

References

• Timokhin A. N., 2010, MNRAS, 408, L41 [ADS]
• Timokhin A. N., 2007, MNRAS, 379, 605 [ADS]
• Timokhin A. N., 2007, Ap&SS, 308, 575 [ADS]
• Timokhin A. N., 2006, MNRAS, 368, 1055 [ADS]

Magnetar magnetosphere

In the power spectrum of Soft Gamma Repeater emission during the tail phase of giant flares one can sometimes see several distinct features which are interpreted as signatures of neutron star oscillations. If these features are indeed due to seismic vibrations of neutron star, this offers an unique opportunity for testing models of neutron star internal structure. To be sure of the driving process it is important to know how oscillations of the neutron star surface modulate the magnetospheric emission.

I and my collaborators suggested a model for the quasiperiodic component of magnetar emission during the tail phase of giant flares. The model invokes modulation of the particle number density in the magnetosphere of magnetar due to changing magnetospheric currents; the magnetospheric currents are modulated by torsional motion of the neutron star surface. I developed an axisymmetric analytical model for the structure of magnetosphere of an oscillating neutron star and calculated the angular distribution of the optical depth to the resonant Compton scattering. The anisotropy of the optical depth may be why QPO are observed only at particular rotational phases.

Figures below illustrate some of the obtained results

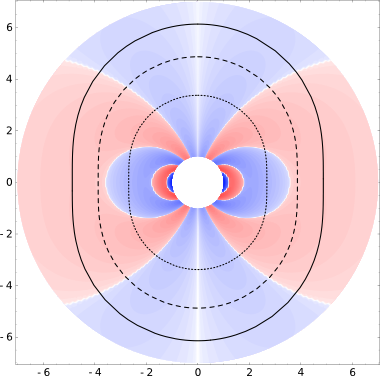
Figure 1 Current density distribution in the magnetosphere of a NS with dipole magnetic field oscillating in toroidal mode (l=10,m=0). The intensity of color in each point is proportional to |j(r,θ)|^1/6 (this moderates contrast of the plot). Positive values of the current density are shown by red colors, negative ones by the blue color. Black lines show the resonant surfaces for three photon energies E=5;10;30 keV — solid, dashed and dotted lines correspondingly. The magnetic field at the pole is assumed to be B₀=10¹⁴G.

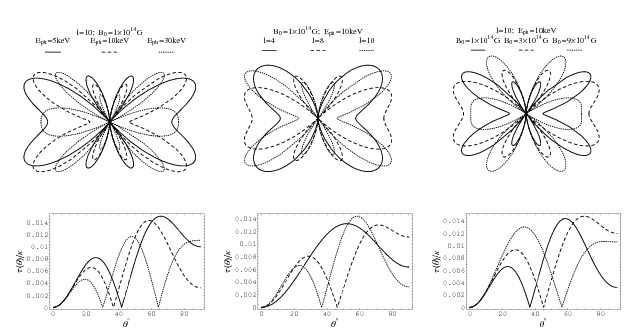
Figure 2 Angular distribution of the optical depth to resonant Compton scattering for radially moving photons in the magnetosphere of an oscillating NS for oscillations with the amplitude of ξ=0.01R_NS. In the upper panels the angular distribution τ(θ)/κ is shown in polar coordinates (τ(θ)/κ,θ), in lower panels the same distribution is shown as a plot τ(θ) for θ∈[0,90°]. In the left panels the optical depth is shown for 3 different initial energies of the scattered photons (E=5;10;30 keV), the magnetic field B₀=10¹⁴G and the harmonic number of the toroidal mode l=10 are fixed. In the middle panels the optical depth is shown for 3 different modes (l=4;6;10), the magnetic field B₀=10¹⁴G and the initial energy of the scattered photons E=10 keV are fixed. In the right panels the optical depth is shown for 3 different values of the NS magnetic field (B₀=1;3;9×10¹⁴G), the harmonic number of the toroidal mode l=10 and the initial energy of the scattered photons E=10 keV are fixed.

References

• Timokhin A. N., Eichler D. and Lyubarsky Yu., 2008, ApJ, 680, 1398 [ADS]